Link to the sign-up page
Mathematical modeling is a subject best learned by doing, like driving a car or cooking. Students will work in groups to study host-parasite dynamics. Groups will come up with a biological question to investigate, derive a mathematical model for the system, and conduct an analysis appropriate for answering the question. Very few marks will be based on the results of the analysis: sometimes, in the process of mathematical modeling, you get really interesting results, and sometimes not. The primary learning goals of this course will be met by demonstrating the ability to translate an interesting, tractable biological question into a mathematical model, coming up with an appropriate analysis, and writing about that model in an intelligible way.
This project will require students to do research outside of class. This research will help identify an appropriate biological question. It may also be necessary to do some research to figure out how to analyze the model, as this class will obviously not cover every technique available for model analysis. Communication and feedback will help to identify problems that are likely to be tractable. It will often be the case that the techniques necessary are easily learned, once one knows where to look!
A really useful approach to finding a problem, borrowed from Steve Ellner's book Dynamic Models in Biology (with John Guckenheimer), is to find a published research paper that uses mathematical modelling to address a question that you find interesting, and then extend that model. That is, come up with a question that was not addressed in the original study, and then extend the original model or the analysis to address that question. The benefit of taking this approach is that you can implement the original model and try to reproduce all of the results presented in the paper - by doing so, you can confirm that you are on the right track.
The marks on this project will be split between four components (click here for more details):
Constraining the project to host-parasite dynamics is not meant to restrict your creativity, but to give it reasonable bounds in which to explore. As you can see from the list of topics below, there are a huge number of interesting areas of research within this seemingly narrow subject. This constraint will also help with peer evaluation, as you will be more knowledgable, and therefore more able to assist one another. However, this restriction is not absolute. Any group wishing to work on a project in another area of biology is free to do so - simply come and talk to me directly so we can identify a likely topic within that area.
To help with group formation, below is a list of potential topics within the area of host-parasite dynamics. On 11 September 2014, part of lecture will be spent discussing the project and facilitating group formation.
Mathematical modeling is a subject best learned by doing, like driving a car or cooking. Students will work in groups to study host-parasite dynamics. Groups will come up with a biological question to investigate, derive a mathematical model for the system, and conduct an analysis appropriate for answering the question. Very few marks will be based on the results of the analysis: sometimes, in the process of mathematical modeling, you get really interesting results, and sometimes not. The primary learning goals of this course will be met by demonstrating the ability to translate an interesting, tractable biological question into a mathematical model, coming up with an appropriate analysis, and writing about that model in an intelligible way.
This project will require students to do research outside of class. This research will help identify an appropriate biological question. It may also be necessary to do some research to figure out how to analyze the model, as this class will obviously not cover every technique available for model analysis. Communication and feedback will help to identify problems that are likely to be tractable. It will often be the case that the techniques necessary are easily learned, once one knows where to look!
A really useful approach to finding a problem, borrowed from Steve Ellner's book Dynamic Models in Biology (with John Guckenheimer), is to find a published research paper that uses mathematical modelling to address a question that you find interesting, and then extend that model. That is, come up with a question that was not addressed in the original study, and then extend the original model or the analysis to address that question. The benefit of taking this approach is that you can implement the original model and try to reproduce all of the results presented in the paper - by doing so, you can confirm that you are on the right track.
The marks on this project will be split between four components (click here for more details):
- Proposal (10%, due 10 October 2014)
- Rough draft (20%, due 7 November 2014)
- Peer review (10%, due 14 November 2014)
- Final draft (50%, due 3 December 2014)
- Group review (10%, due 3 December 2014)
Constraining the project to host-parasite dynamics is not meant to restrict your creativity, but to give it reasonable bounds in which to explore. As you can see from the list of topics below, there are a huge number of interesting areas of research within this seemingly narrow subject. This constraint will also help with peer evaluation, as you will be more knowledgable, and therefore more able to assist one another. However, this restriction is not absolute. Any group wishing to work on a project in another area of biology is free to do so - simply come and talk to me directly so we can identify a likely topic within that area.
To help with group formation, below is a list of potential topics within the area of host-parasite dynamics. On 11 September 2014, part of lecture will be spent discussing the project and facilitating group formation.
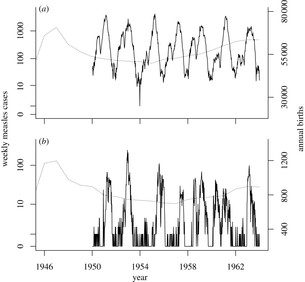
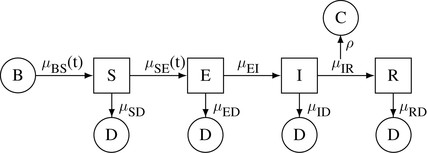
- Dynamics of a particular infectious disease
- Sexually-transmitted diseases
- Vector-transmitted diseases
- Optimal vaccination strategies
- Spatial spread of disease
- Effect of host heterogeneity (e.g., super-spreaders, host age structure)
- Within-host dynamics (e.g., immune-parasite interaction)
- Evolution of host resistance
- Evolution of virulence
- Multi-host and/or multi-pathogen systems
- Community ecology of disease (e.g. interactions between parasites and predators)
- Stochastic disease dynamics